Before moving on to the final part of this series on solar irradiance and solar PV power across Alberta, I wanted to do a little segway and talk about how albedo is a particularly relevant issue for the workings of PV panels in Alberta and similar places. This is also in part a short elaboration/commentary on a presentation I heard as part of a webinar organised by Solar Alberta on February 25.
Let me say: if you'd rather just jump to the bit which has R codes to download the relevant data, then please just click here . If you're wondering what albedo is, please read on.
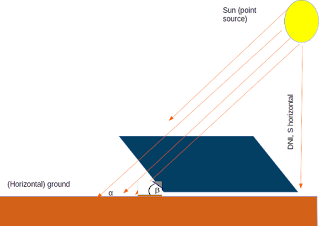
In the earlier blog post, what I did was to model the amount of solar insolation at a given site through the "Global Horizontal Irradiation," or GHI, which is a measure of the amount of solar energy that falls on a horizontally flat solar panel that is "looking up". GHI is in turn made up of two separate components. The larger of these is the component of the solar insolation which falls more or less straight down, also known as Direct Normal Irradiance or "DNI". A second component however is made up of the solar insolation which hits the panel after bouncing off of the atmosphere and, especially in the case of PV panels deployed in urban settings, of large, reflective structures.
Finally, it's worth considering also what happens when the solar PV panel is--as is typical--tilted. In that case, the total solar irradiation on the PV panel--in the "plane of array"--is the sum of three distinct components, one of which is the component which falls directly on the panel in a normal from the sun; a second component which is diffuse solar radiation from the atmosphere and which lands on the tilted panel; and a third component which is reflected off of the ground and meets the panel. Programmatically, this is just:
G
total = G
DNI + G
DIFF + G
ground
A really good way to understand these different components is to read the explanations of various (competing) models of POA irradiance models on the
Sandia website. For my purposes, I will use the following conversions:
-
Beam irradiance, GBeam
- The beam irradiance is a product of the cosine of the tilt angle (θ) and the DNI: Gbeam = GDNI
*cos(θ)
- Ground reflected component, GGround
- The ground reflected component is going to similarly be a function of the tilt angle but also an "albedo" constant, ρ ,which we can quantify for each month at each location. Note the definition of albedo right there: it's simply a two-dollar word for how much light is reflected off a particular piece of ground.
-
Diffuse component, GDIFF
- Let me just refer you back to the Sandia website. I'll be frank, there are too many competing models to compute how much solar irradiance is diffuse in the atmosphere above a certain site at a given time, and I'd rather just focus on crunching out the numbers for this blog post. I will simply download the diffuse irradiance below.
Let me just point out, once again: it's important not to confuse the GHI and DNI types of irradiance. The latter is the bit which falls directly downwards on a flat solar PV panel, while the former includes other components.
Also, you're possibly wondering about the full title of this blog post. Here's a picture of my transition type glasses which I took on my Edmonton balcony the other (not very sunny) day. What could the fact of the transitions having faded to black on a not-so-sunny day got to do with solar PV electricity and its availability? Quite a lot!
Finally, before moving on to the R code, I should probably point out that we will make use of a specific way to calculate the tilt angle. As with so many things, there are multiple approaches to calculating a tilt angle, which in general factor in the latitude of a given location and a temporal factor. Depening on your desired level of exactness, this temporal factor can vary from month, day or even hour: it is meant to account for the changes in the solar azimuth angle and the location of the PV panel. You can find papers which compare multiple models for calculating the optimal tilt angle for a given location, such as
this one from Palestine. For Western Canada--which we've defined here as just the provinces of British Columbia and Alberta--the latitudes range from 48.56 to 59.07, measuring roughly 1100 kms North-South. Figuring out a specific tilt angle for each location within our dataset, while more "correct," might not be a great use of time for a simple blog post.
One perfectly reasonable compromise I can find is to use the approach in
Stanicu and Stanicu, which is to define the tilt angle θ as the sum of the latitude, φ and declination angle, δ : θ = φ + δ
For its part, the declination angle is a function of the day of the year, d:
δ = -23.45*cos(0.986*(d+10))
In a later part of this post, I will show how this can be coded into R.
The R Codes
From here on, I'm just going to focus on the mechanics of downloading the data and presenting it in the same way as I did last time. Once finished, I will show how albedo--due largely to snow cover--makes the question of solar insolation and, eventually, PV electricity, in Alberta more nuanced than would be thought about if all you did is look at GHI.
In the next code snippet, I am going to first load all of the R packages I need and then move on from there to add names to the "Census Divisions" in Alberta.
library(rgeos)
library(maptools)
library(ggmap)
library(ggplot2)
library(sp)
library(rgdal)
library(raster)
library(nasapower)
library(scales)
library(plyr)
alberta_division_names = c("Medicine Hat", "Lethbridge", "Claresholm", "Hanna", "Strathmore", "Calgary", "Wainwright", "Red Deer", "Rocky Mountain House", "Lloydminster", "Edmonton", "Cold Lake", "White Court", "Hinton", "Canmore", "Fort McMurray", "Slave Lake", "Grande Cache", "Grande Prairie")
#We want to be able to combine/compare these with the districts in British Columbia
western_canada_province_names = western_canada_ellipsoid@data$NAME_1
western_canada_division_names = c(alberta_division_names, western_canada_ellipsoid@data$NAME_2[20:47])
western_canada_district_names = c(alberta_division_names, western_canada_ellipsoid@data$NAME_2[20:47])
western_canada_albedo_annual = cbind(western_canada_district_names, western_canada_albedo_monthly[,13])
Next, one straightforward thing is to use
nasapower to download values for the diffuse solar irradiation and also the surface albedo constant. The "parameter," or keyword, which nasapower uses to define these values are "DIFF" and "SRF_ALB", and to turn these into dataframes. As always, I am using the "CLIMATOLOGY" timeframe which takes monthly averages for the period between 1984 and 2013 and the "SSE" community which specifies that the units used will be useful for the renewable energy community.
In the code snippet below: I create distinct data.frame objects which cover all of the sets of data that we want. Unlike in the previous post, I am just going to treat "Western Canada" as one single unit here and from there . I download both sets of data for each site in our dataset. From there, I divide each request from the server into separate data.frame. Finally, I populate each row of the dedicated data frames with the relevant retrieved data.
One thing you'll notice is that I do two separate requests: one for the GHI alone and one for the albedo, DNI/DNR and Diffuse components combined. This is purely because the API request only allows a maximum of three parameters to be downloaded at once if you're using the "CLIMATOLOGY" timeframe. Next, I should point out that while I also downloaded GHI radiation last time, that was limited to using annual values. Later on, it will become clear why monthly data are also valuable for this blog post.
#We want four types of data on a monthly basis for each site: albedo constants as well as GHI, DNR (aka DNI) and Diffuse insolation
western_canada_dnr_monthly = data.frame(matrix(ncol = 13, nrow = nrow(western_canada_coordinates)))
western_canada_ghi_monthly = data.frame(matrix(ncol = 13, nrow = nrow(western_canada_coordinates)))
western_canada_albedo_monthly = data.frame(matrix(ncol = 13, nrow = nrow(western_canada_coordinates)))
western_canada_diffuse_monthly = data.frame(matrix(ncol = 13, nrow = nrow(western_canada_coordinates)))
for(i in 1:nrow(western_canada_coordinates))
{
#Get the data from NASA POWER
#Make sure to use the correct parameter names from nasapower
#retrieved_parameters = nasapower::get_power(community = "SSE", pars = c("DNR", "DIFF","SRF_ALB"), lonlat = c(western_canada_coordinates[i,1],
#See the explanation above for why we do this with two requests western_canada_coordinates[i,2]), temporal_average = "CLIMATOLOGY")
retrieved_global_horizontal = nasapower::get_power(community = "SSE", pars ="ALLSKY_SFC_SW_DWN", lonlat = c(western_canada_coordinates[i,1],
western_canada_coordinates[i,2]), temporal_average = "CLIMATOLOGY")
#Split the API request into separate data.frames
#Notice that the original request returns a tibble, which is more information than we want/need
#Once we divide it into 4 data.frames, we fill one row of each of the data.frames we want
retrieved_albedo = data.frame(retrieved_parameters[which(retrieved_parameters$PARAMETER == "SRF_ALB"),])
retrieved_diffuse = data.frame(retrieved_parameters[which(retrieved_parameters$PARAMETER == "DIFF"),])
retrieved_dnr = data.frame(retrieved_parameters[which(retrieved_parameters$PARAMETER == "DNR"),])
retrieved_ghi = data.frame(retrieved_global_horizontal[which(retrieved_global_horizontal$PARAMETER == "ALLSKY_SFC_SW_DWN"),])
#Since we've set up data.frames for the information/data we need, populate each row of those two data.frames
western_canada_albedo_monthly[i,] = retrieved_albedo[,4:16]
western_canada_diffuse_monthly[i,] = retrieved_diffuse[,4:16]
western_canada_dnr_monthly[i,] = retrieved_dnr[,4:16]
western_canada_ghi_monthly[i,] = retrieved_ghi[,4:16]
#Just a quick check
print(paste("Ya habeebi, we are at site", i, sep = ", "))
}
We now have monthly averages for the DNR, the Albedo constant and the diffuse irradiation/insolation for each of the 47 Level 2 districts in Western Canada. As with the previous post, the data is gathered based on the longitude and latitude coordinates of the centroids of each district, using the NASA POWER package from Cran. Doubtlessly, using the centroids for each of these districts is probably introducing at least some kind of errors--you wouldn't necessarily want to place solar panels there unless you've determined that doing so is coincidentally the optimal location for solar radiation. I might re-visit this in a later blog spot, but for now this will do.
One thing which I never quite liked but have found efficient is the very "tight" syntax for subsetting data.frames: your_subset = your_data_frame[which(your_data$COLUMN_NAME == "your criterion",)]. If you're confused about why I chose columns 4:16, please see the previous post.
How to compute the tilt angles per site per month? In the snippet below, I define what the "median day" per month is. I then calculate straight away what the tilt angle is for that median day.
days_in_months = c(31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31)
#Now we want is to know what the median number of days
midpoint_of_months = ceiling(0.5*days_in_months)
#Now, to find the median day of each month as out of the day
cumulative_days_months = cumsum(days_in_months)
median_days_of_months = vector(length = 12)
median_days_of_months[1] = midpoint_of_months[1]
for(i in 2:12)
{
#We start with the previous month and then add to it to the median number
#of days from the present month
median_days_of_months[i] = cumulative_days_months[i-1] + midpoint_of_months[i]
}
It's important to make clear that R computes trignometric functions using radians while so far we've been assuming that it's degrees. Below, I create a simple function which turns degrees into radians and then finally returns a monthly tilt angle for each of the Level 2 sub-divisions in Western Canada.
#Make a function that takes degrees and returns radians
deg_to_rad <- function(degrees)
{
rads_to_return = degrees*pi/180
return(rads_to_return)
}
#Defining the declination angles
#Define the number of days per month
days_in_months = c(31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31)
#Now we want is to know what the median number of days
midpoint_of_months = ceiling(0.5*days_in_months)
#Now, to find the median day of each month as out of the day
cumulative_days_months = cumsum(days_in_months)
median_days_of_months = vector(length = 12)
median_days_of_months[1] = midpoint_of_months[1]
for(i in 2:12)
{
#We start with the previous month and then add to it to the median number
#of days from the present month
median_days_of_months[i] = cumulative_days_months[i-1] + midpoint_of_months[i]
}
#Declination angles, change only by month
declinations_monthly = vector(length = 12)
for(i in 1:12)
{
declinations_monthly[i] = deg_to_rad(-23.45*cos(deg_to_rad(0.986*(median_days_of_months[i]+10))))
}
#Now create a data.frame holding a monthly value of the optimal tilt angle
#for each site
tilt_angles_western_canada = data.frame(ncol = 12, nrow = nrow(western_canada_coordinates))
for(i in 1:nrow(western_canada_coordinates))
{
for(j in 1:12)
{
tilt_angles_western_canada[i,j] = deg_to_rad(western_canada_coordinates[i,2]) + declinations_monthly[j]
}
}
Now with the monthly tilt angles, we can compute the tilted insolation/irradiance per site per month, this is called a "Plane of Array" (POA) irradiance, as discussed above. The code snippet below implements the straightforward equation I copied in the earlier part of this blog post. Note that we will leave out the consideration of "annual" values for now--for reasons that will eventually become obvious.
calculate_poa_monthly <- function(tilt_angles, ghi_values, dnr_values, diffuse_values, albedo_values)
{
poa_monthly_values = data.frame(matrix(nrow = nrow(tilt_angles), ncol = 12))
for(i in 1:nrow(tilt_angles))
{
for(j in 1:12)
{
#Bring this out here to simplify the spaghetti below
tilt_inner_part = cos(tilt_angles[i,j])
poa_part_1 = dnr_values[i,j]*tilt_inner_part
poa_part_2 = ghi_values[i,j]*albedo_values[i,j]*0.5*(1- tilt_inner_part)
poa_part_3 = diffuse_values[i,j]
poa_monthly_values[i,j] = poa_part_1 + poa_part_2 + poa_part_3
}
}
return(poa_monthly_values)
}
#Execute this function with the data we have now
western_canada_poa = calculate_poa_monthly(tilt_angles_western_canada, western_canada_ghi_monthly, western_canada_dnr_monthly, western_canada_diffuse_monthly, western_canada_albedo_monthly)
To avoid an ugly headache: keep in mind that we've already converted the units for the tilt angles from
At this point, let's say we wanted to just do something nice and pretty like the map from the last time. Just simply show the Level 2 districts in Alberta + British Columbia and then plot them, just like last time. In the code snippet below, I am going to repeat the same steps, more or less, like last time and the post a map showing a map of the POA insolation across the 47 Level 2 districts of Western Canada. In the section following that, we're going to go over some of the seasonal and regional trends of the POA across Alberta and British Columbia.
#Create the vector of annual values of the POA
annual_poa_western_canada = rowSums(days_in_months*western_canada_poa)
western_canada_annual_poa = data.frame(unique(western_canada_ellipsoid@data$NAME_2), annual_poa_western_canada)
colnames(western_canada_annual_poa) = c("NAME_2", "Insolation")
#This is where we got the projected maps of Alberta + BC
western_canada_ellipsoid = canada_level2_ellipsoid[which(canada_level2_ellipsoid$NAME_1 == "Alberta" | canada_level2_ellipsoid$NAME_1 == "British Columbia"),]
#Give each row an ID
western_canada_ellipsoid@data$id = rownames(western_canada_ellipsoid@data)
#Join the POA insolation data to the geographical data.frame
western_canada_ellipsoid@data = join(western_canada_ellipsoid@data, western_canada_annual_poa, by = "NAME_2")
#Now we create a data.frame which can be projected using ggplot2
#Note it has 661,178 rows!
western_canada_fortified <- fortify(western_canada_ellipsoid)
#...but we want to make sure that it has the correct data attached to it, showing the POA insolation
western_canada_fortified <- join(western_canada_fortified, western_canada_ellipsoid@data, by = "id")
the_plot <- ggplot() + geom_polygon(data = western_canada_fortified, aes(x = long, y = lat, group = group, fill = Insolation), color = "black", size = 0.15, show.legend = TRUE) + scale_fill_distiller(name="POA insolation, annual \n kWh per m^2", palette = "Spectral", breaks = pretty_breaks(n = 9))
...and this is what the map now looks like.
A couple of small things this time. Firstly, I created the map/plot as an object "the_plot" and then executed that through the Console. I'm not sure why, but there seems to be some kind of long-running bug with ggplot which is avoided by this facile trick. Secondly, this time I calculated the annual insolation by multiplying each row of the monthly POA data.frame by the number of days in a month and then summing. That bit should have been straightforward.
I find the above map aesthetically pleasing, but there's a limit to the kind of story you can tell with this sort of image. There are of course the same caveats from last time: the districts themselves are quite large, and pretending that the same insolation regimes and tilt angles are valid throughout a Level 2 district will have its limitations. On another note, this single "snapshot" of annual data tells us little about how albedo from snow impacts different parts of Western Canada.
So, quantitatively, how much does the consideration of albedo actually change things? Well, I'll make a data table comparing the GHI and POA insolations, on a yearly basis, for each of the sites. You could install the "data.table" package for this; if you'd prefer not to, then you could create any old data.frame but data tables do make things simpler down the road.
display_insolations = data.table(western_canada_district_names, western_canada_solar_insolation_annual, western_canada_annual_poa[,2], keep.rownames = FALSE)
colnames(display_insolations) = c("District name", "GHI", "POA")
#Print it out and have a look
> display_insolations
District name GHI POA
1: Medicine Hat 1343.20 1469.381
2: Lethbridge 1193.55 1393.421
3: Claresholm 1182.60 1391.090
4: Hanna 1153.40 1359.715
5: Strathmore 1149.75 1365.419
6: Calgary 1157.05 1383.741
7: Wainwright 1233.70 1421.541
8: Red Deer 1105.95 1286.419
9: Rocky Mountain House 1131.50 1301.670
10: Lloydminster 1135.15 1361.056
11: Edmonton 1168.00 1341.603
12: Cold Lake 1332.25 1463.725
13: White Court 1332.25 1474.018
14: Hinton 1266.55 1435.325
15: Canmore 1262.90 1439.510
16: Fort McMurray 1251.95 1435.881
17: Slave Lake 1222.75 1406.745
18: Grande Cache 1222.75 1409.017
19: Grande Prairie 1219.10 1410.113
20: Alberni-Clayoquot 1197.20 1469.776
21: Bulkley-Nechako 1171.65 1363.674
22: Capital 1241.00 1484.624
23: Cariboo 1237.35 1411.877
24: Central Coast 1138.80 1413.606
25: Central Kootenay 1324.95 1467.803
26: Central Okanagan 1332.25 1466.766
27: Columbia-Shuswap 1233.70 1432.005
28: Comox-Strathcona 1208.15 1451.819
29: Cowichan Valley 1204.50 1477.752
30: East Kootenay 1361.45 1461.900
31: Fraser-Fort George 1131.50 1372.002
32: Fraser Valley 1273.85 1465.747
33: Greater Vancouver 1259.25 1471.242
34: Kitimat-Stikine 1040.25 1332.545
35: Kootenay Boundary 1332.25 1474.285
36: Mount Waddington 1109.60 1436.950
37: Nanaimo 1197.20 1476.098
38: North Okanagan 1270.20 1456.289
39: Northern Rockies 1087.70 1267.006
40: Okanagan-Similkameen 1273.85 1471.606
41: Peace River 1138.80 1318.155
42: Powell River 1208.15 1450.495
43: Skeena-Queen Charlotte 1058.50 1375.758
44: Squamish-Lillooet 1270.20 1447.448
45: Stikine 1062.15 1272.082
46: Sunshine Coast 1259.25 1460.586
47: Thompson-Nicola 1270.20 1436.779
Is there a difference across the districts in how much albedo adds to the insolation and, if so, does that happen at specific times of year?
If one defines the proportion of ground reflected insolation to total (POA) insolation, then we can simply plot that against months of the year. For our dataset, the proportion of ground reflected insolation to the total POA insolation varies from 0.44% to 9.5%; but both of these values are hit in the same location, in the "Northern Rockies" district of British Columbia (longitude and latitude of the centroid: 123.44 West and 59.07 North). These points occur at December and June, respectively; clearly, the GHI component is the major defining feature of this insolation.
In general, this is equally true for both Alberta and British Columbia; the months during which ground-reflected radiation accounts for the highest possible proportion of the total POA insolation are determined by the GHI. This is shown in the next picture and detailed in the following code snippet.
We arrived here through:
ground_reflected_insolation = data.frame(matrix(nrow = nrow(western_canada_coordinates), ncol = 12))
for(i in 1:47)
{
for(j in 1:12)
{
ground_reflected_insolation[i,j] = western_canada_albedo_monthly[i,j]*western_canada_ghi_monthly[i,j]*(0.5*(1-cos(tilt_angles_western_canada[i,j])))
}
}
ground_reflected_to_poa = data.frame(matrix(nrow = nrow(western_canada_coordinates), ncol = 12))
ground_reflected_to_ghi = data.frame(matrix(nrow = nrow(western_canada_coordinates), ncol = 12))
for(i in 1:47)
{
for(j in 1:12)
{
ground_reflected_to_poa[i,j] = ground_reflected_insolation[i,j]/western_canada_poa[i,j]
ground_reflected_to_ghi[i,j] = ground_reflected_insolation[i,j]/western_canada_ghi_monthly[i,j]
}
}
for(i in 1:47)
{
for(j in 1:12)
{
if(ground_reflected_to_poa[i,j] == min(ground_reflected_to_poa))
{
print(paste(i,j, sep = ", "))
}
}
}
for(j in 1:12)
{
for(i in 1:47)
{
if(ground_reflected_to_poa[i,j] == max(ground_reflected_to_poa[,j]))
{
print(paste(i,j, sep = ", "))
print(western_canada_district_names[i])
}
}
}
ground_to_poa_bc = vector(length = 12)
ground_to_poa_ab = vector(length = 12)
ground_to_ghi_ab = vector(length = 12)
ground_to_ghi_bc = vector(length = 12)
for(j in 1:12)
{
ground_to_poa_ab[j] = mean(ground_reflected_to_poa[1:19,j])
ground_to_poa_bc[j] = mean(ground_reflected_to_poa[20:47, j])
ground_to_ghi_ab[j] = mean(ground_reflected_to_ghi[1:19, j])
ground_to_ghi_bc[j] = mean(ground_reflected_to_ghi[20:47, j])
}
plot(ground_to_ghi_ab, type = "b", pch = 12, col = "red", ylab = "", xlab = "Month")
lines(ground_to_ghi_bc, type = "b", pch = 12, col = "green")
legend(2, 0.06, legend = c("Alberta", "BC"), col = c("red", "green"), pch = 12)
title(main = "Ground reflected insolation as a proportion of POA \n")
Some Closing Remarks
So I started out hoping to "prove" that snow cover in some Alberta districts would more or less compensate for the reduced GHI during in the winter months. While that does not seem to be the case--ie, I was wrong--I think there is still space to dig a bit deeper in the next blog post, where I will also examine questions such as length of daylight hours, temperatures and how these correlate to give us not only insolation/irradiance but also PV yield, measured in kWh. I also stopped short of doing a regression analysis of insolation as a function of latitude as I did not think it would be helpful in this limited case of Alberta and BC, although there is some evidence that looking at PV yield as a function of elevation/altitude is a separate but good idea.
Finally, some people who read this will probably be frustrated that I have used insolation and irradiance more or less interchangably. Please note that I have used "insolation" to refer to an amount of energy radiating downwards and measured in kWh (less often Wh) or Joules (kJ, MJ, etc). Where I did not think it would make too much of a difference however, I did not mind using "irradiance" or simply "radiation" although, of course, that will not do in the blog post coming up.
